내가 다시 보려고 만든 “밑바닥 부터 시작하는 딥러닝” 정리 3
책 “밑바닥부터 시작하는 딥러닝 1권” 내용 중 다시 보려고 만든 자료입니다. (챕터 5)
chapter 5
- 챕터 4에서는 신경망 학습에 대해서 설명했다. 그때 신경망의 가중치 매개변수의 기울기(정확히는 가중치 매개변수에 대한 손실 함수의 기울기)는 수치 미분을 사용해 구했다.
- 이번 챕터에서는 가중치 매개변수의 기울기를 효율적으로 계산하는 “오차역전파법(backpropagation)”을 배워보겠다.
- 순전파는 계산 그래프의 출발점부터 종착점으로의 전파이고, 역전파는 반대방향 전파이다. 역전파는 이후에 미분을 계산할 때 중요한 역할을 한다.
chapter 5.1.2 국소적 계산
- 계산 그래프는 국소적 계산에 집중한다.
- 국소적인 계산은 단순하지만, 그 결과를 전달함으로써 전체를 구성하는 복잡한 계산을 해낼 수 있다.
chapter 5.1.3 왜 계산 그래프로 푸는가 ?
- 첫 번째, ‘국소적 계산’ 때문
- 두 번째, 계산 그래프는 중간 계산 결과를 모두 보관할 수 있다.
- 세 번째, 실제 계산 그래프를 사용하는 가장 큰 이유는 역전파를 통해 ‘미분’을 효율적으로 계산할 수 있는 점에 있다. 중간까지 구한 미분 결과를 공유할 수 있어서 다수의 미분을 효율적으로 계산할 수 있다. 이처럼 계산 그래프의 이점은 순전파와 역전파를 활용해서 각 변수의 미분을 효율적으로 구할 수 있다는 것이다.
chapter 5.2 연쇄법칙
- ‘국소적 미분’을 전달하는 원리는 연쇄법칙에 따른 것이다.
- 연쇄법칙은 합성 함수의 미분에 대한 성질이며, “합성 함수의 미분은 합성 함수를 구성하는 각 함수의 미분의 곱으로 나타낼 수 있다.”라는 정의를 가진다.
chapter 5.5 활성화 함수 계층 구현하기
- relu
- relu의 수식
- relu의 수식에서 x에 대한 y의 미분
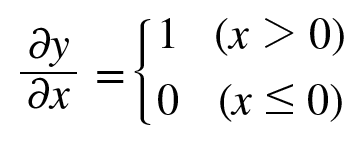
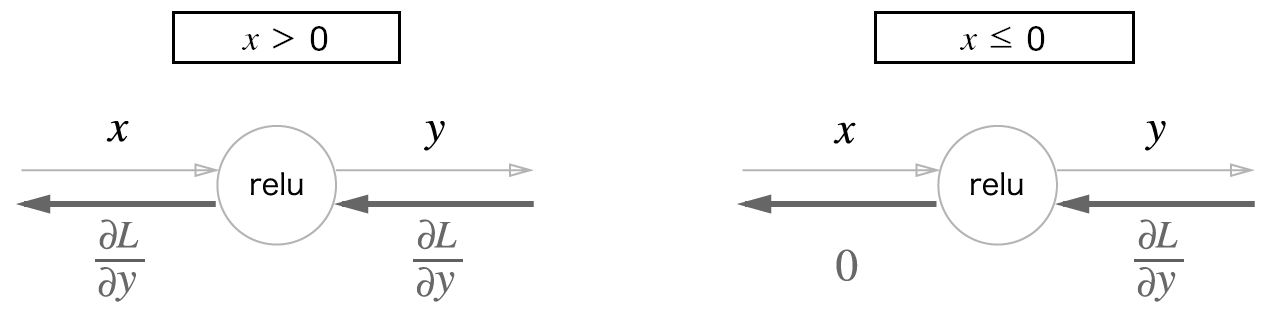
- relu 계층의 계산 그래프
- sigmoid
- 시그모이드 수식
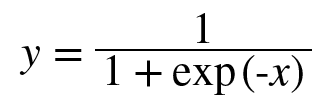
- 시그모이드 계층의 계산그래프 (간소화)
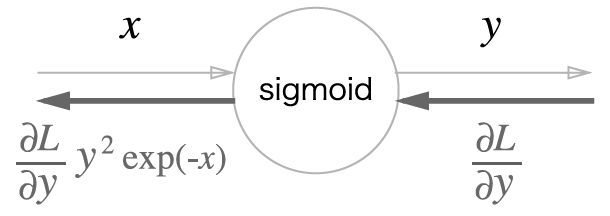
- dL/dy * y^2 * exp(-x)은 다음처럼 정리해서 쓸 수 있다.
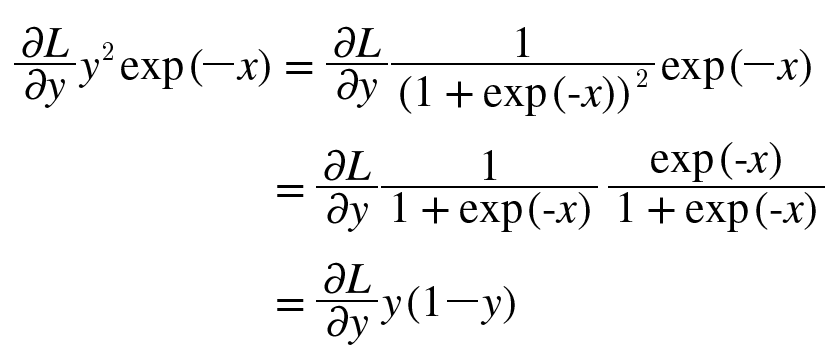
chapter 5.6.1 Affine 계층
- 신경망의 순전파 때 수행하는 행렬의 곱은 기하학에서는 어파인 변환이라고 한다. 이 책에서는 어파인 변환을 수행하는 처리를 ‘Affine 계층’ 이라는 이름으로 구현한다.
chapter 5.6.3 Softmax-with-Loss 계층
손실 함수인 교차 엔트로피 오차도 포함하여 ‘Softmax-with-Loss 계층’이라는 이름으로 구현한다.
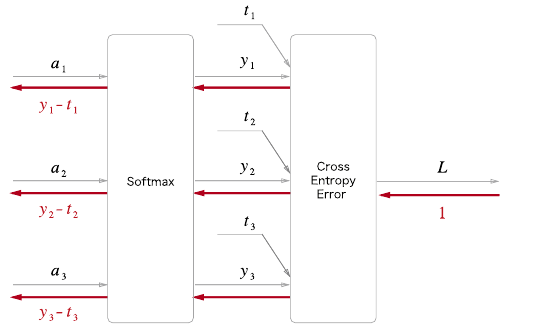
‘소프트맥스 함수’의 손실 함수로 ‘교차 엔트로피 오차’를 사용하니 역전파가 (y1-t1, y2-t2, y3-t3)로 말끔히 떨어진다. 이런 말끔함은 우연이 아니라 교차 엔트로피 오차라는 함수가 그렇게 설계되었기 때문이다. 또한, 회귀의 출력층에서 사용하는 ‘항등 함수’의 손실 함수로 ‘오차 제곱합’을 이용하는 이유도 이와 같다. 즉 ‘항등 함수’의 손실 함수로 ‘오차제곱합’을 사용하면 역전파의 결과가 (y1-t1, y2-t2, y3-t3)로 말끔히 떨어진다.
예를 하나 들어보자. 정답 레이블이 (0,1,0)일 때 softmax 계층이 (0.3, 0.2, 0.5)를 출력했다면 ? 정답 레이블을 보면 정답의 인덱스는 1이다. 그런데 출력에서는 이때의 확률이 겨우 0.2 라서, 이 시점의 신경망은 제대로 인식하지 못하고 있다. 이 경우 softmax 계층의 역전파는 (0.3, -0.8, 0.5)라는 커다란 오차를 전파한다. 결과적으로 softmax 계층의 앞 계층들은 그 큰 오차로부터 큰 깨달음을 얻게 된다.
chapter 5.7.1 신경망 학습의 전체 그림
- 전체 : 신경망에는 적응 가능한 가중치와 편향이 있고, 이 가중치와 편향을 훈련 데이터에 적응하도록 조정하는 과정을 ‘학습’이라 한다. 신경망 학습은 다음과 같이 4단계로 수행한다.
- 1단계(미니배치) : 훈련 데이터 중 일부를 무작위로 가져온다. 이렇게 선별한 데이터를 미니배치라 하며, 그 미니배치의 손실 함수 값을 줄이는 것이 목표
- 2단계(기울기 산출) : 미니배치의 손실 함수 값을 줄이기 위해 각 가중치 매개변수의 기울기를 구한다. 기울기는 손실 함수의 값을 가장 작게 하는 방향을 제시한다.
- 3단계(매개변수 갱신) : 가중치 매개변수를 기울기 방향으로 아주 조금 갱신
- 4단계(반복) : 1~3단계를 반복한다.
- 지금까지 설명한 오차역전파법이 등장하는 단계는 두 번째인 ‘기울기 산출’입니다. 앞장에서는 이 기울기를 구하기 위해서 수치 미분을 사용했다. 그런데 수치 미분은 구현하기는 쉽지만 계산이 오래 걸렸다. 오차역전파법을 이용하면 느린 수치 미분과 달리 기울기를 효율적이고 빠르게 구할 수 있다.
chapter 5.7.3 오차역전파법으로 구한 기울기 검증하기
수치 미분은 느리다. 그리고 오차역전파법을 제대로 구현해두면 수치 미분은 더 이상 필요가 없다. 그러면 수치 미분은 진짜 쓸모가 없을까? 사실은 수치 미분은 오차 역전파법을 정확히 구현했는지 확인하기 위해서 필요하다.
수치 미분의 이점은 구현하기 쉽다는 것이다. 그래서 수치 미분의 구현에는 버그가 숨어 있기 어려운 반면, 오차 역전파법은 구현하기 복잡해서 종종 실수가 나온다. 그래서 수치 미분의 결과와 오차역전파법의 결과를 비교하여 오차역전파법을 제대로 구현했는지 검증하곤 한다. 이처럼 두 방식으로 구한 기울기가 일치함(엄밀히 말하면 거의 같음)을 확인하는 작업을 기울기 확인이라고 한다.
chapter 5.8 정리
이번 챕터에서는 계산 과정을 시작적으로 보여주는 방법인 계산 그래프를 배웠다. 계산 그래프를 이용해 신경망의 동작과 오차역전파법을 설명하고, 그 처리 과정을 계층이라는 단위로 구현했다. (relu 계층, softmax-with-loss 계층, affine 계층, softmax 계층 등)
모든 계층에서 forward와 backword라는 메서드를 구현한다. 전자는 데이터를 순방향으로 전파, 후자는 역방향으로 전파함으로써 가중치 매개변수의 기울기를 효율적으로 구할 수 있다. 이처럼 동작을 계층으로 모듈화한 덕분에, 신경망의 계층을 자유롭게 조합하여 원하는 신경망을 쉽게 만들 수 있다.

